Balanced Red/Black Tree
For circumstances where sorted containers may become large at runtime, a list becomes problematic due to algorithmic costs of searching it. For these situations, Zephyr provides a balanced tree implementation which has runtimes on search and removal operations bounded at O(log2(N)) for a tree of size N. This is implemented using a conventional red/black tree as described by multiple academic sources.
The rbtree tracking struct for a rbtree may be initialized
anywhere in user accessible memory. It should contain only zero bits
before first use. No specific initialization API is needed or
required.
Unlike a list, where position is explicit, the ordering of nodes
within an rbtree must be provided as a predicate function by the user.
A function of type rb_lessthan_t() should be assigned to the
lessthan_fn field of the rbtree struct before any tree
operations are attempted. This function should, as its name suggests,
return a boolean True value if the first node argument is “less than”
the second in the ordering desired by the tree. Note that “equal” is
not allowed, nodes within a tree must have a single fixed order for
the algorithm to work correctly.
As with the slist and dlist containers, nodes within an rbtree are
represented as a rbnode structure which exists in
user-managed memory, typically embedded within the data structure
being tracked in the tree. Unlike the list code, the data within an
rbnode is entirely opaque. It is not possible for the user to extract
the binary tree topology and “manually” traverse the tree as it is for
a list.
Nodes can be inserted into a tree with rb_insert() and removed
with rb_remove(). Access to the “first” and “last” nodes within a
tree (in the sense of the order defined by the comparison function) is
provided by rb_get_min() and rb_get_max(). There is also a
predicate, rb_contains(), which returns a boolean True if the
provided node pointer exists as an element within the tree. As
described above, all of these routines are guaranteed to have at most
log time complexity in the size of the tree.
There are two mechanisms provided for enumerating all elements in an
rbtree. The first, rb_walk(), is a simple callback implementation
where the caller specifies a C function pointer and an untyped
argument to be passed to it, and the tree code calls that function for
each node in order. This has the advantage of a very simple
implementation, at the cost of a somewhat more cumbersome API for the
user (not unlike ISO C’s bsearch() routine). It is a recursive
implementation, however, and is thus not always available in
environments that forbid the use of unbounded stack techniques like
recursion.
There is also a RB_FOR_EACH iterator provided, which, like the
similar APIs for the lists, works to iterate over a list in a more
natural way, using a nested code block instead of a callback. It is
also nonrecursive, though it requires log-sized space on the stack by
default (however, this can be configured to use a fixed/maximally size
buffer instead where needed to avoid the dynamic allocation). As with
the lists, this is also available in a RB_FOR_EACH_CONTAINER
variant which enumerates using a pointer to a container field and not
the raw node pointer.
Tree Internals
As described, the Zephyr rbtree implementation is a conventional red/black tree as described pervasively in academic sources. Low level details about the algorithm are out of scope for this document, as they match existing conventions. This discussion will be limited to details notable or specific to the Zephyr implementation.
The core invariant guaranteed by the tree is that the path from the root of the tree to any leaf is no more than twice as long as the path to any other leaf. This is achieved by associating one bit of “color” with each node, either red or black, and enforcing a rule that no red child can be a child of another red child (i.e. that the number of black nodes on any path to the root must be the same, and that no more than that number of “extra” red nodes may be present). This rule is enforced by a set of rotation rules used to “fix” trees following modification.
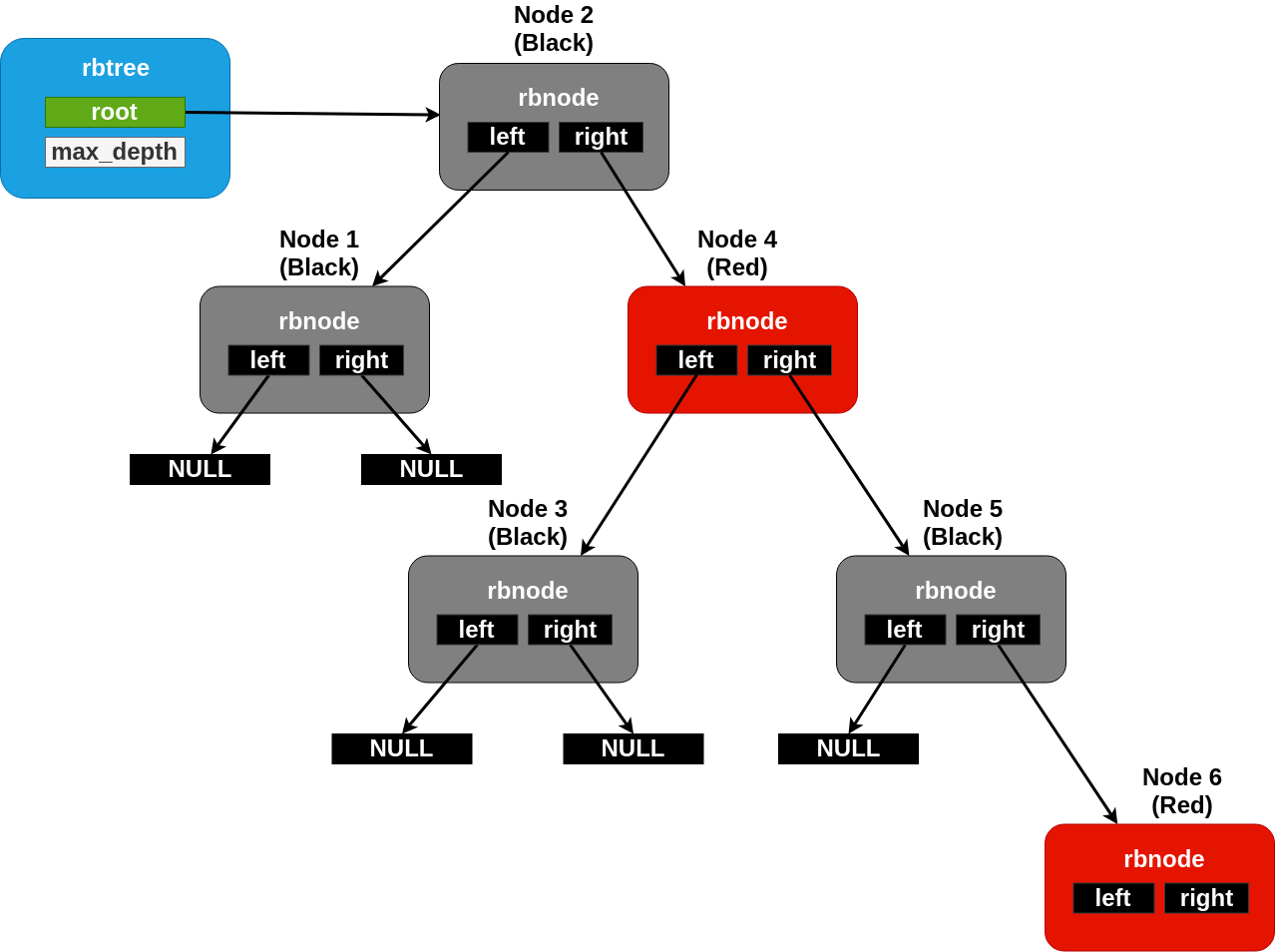
A maximally unbalanced rbtree with a black height of two. No more nodes can be added underneath the rightmost node without rebalancing.
These rotations are conceptually implemented on top of a primitive
that “swaps” the position of one node with another in the list.
Typical implementations effect this by simply swapping the nodes
internal “data” pointers, but because the Zephyr rbnode is
intrusive, that cannot work. Zephyr must include somewhat more
elaborate code to handle the edge cases (for example, one swapped node
can be the root, or the two may already be parent/child).
The rbnode struct for a Zephyr rbtree contains only two
pointers, representing the “left”, and “right” children of a node
within the binary tree. Traversal of a tree for rebalancing following
modification, however, routinely requires the ability to iterate
“upwards” from a node as well. It is very common for red/black trees
in the industry to store a third “parent” pointer for this purpose.
Zephyr avoids this requirement by building a “stack” of node pointers
locally as it traverses downward through the tree and updating it
appropriately as modifications are made. So a Zephyr rbtree can be
implemented with no more runtime storage overhead than a dlist.
These properties, of a balanced tree data structure that works with only two pointers of data per node and that works without any need for a memory allocation API, are quite rare in the industry and are somewhat unique to Zephyr.
Red/Black Tree API Reference
- group rbtree_apis
Balanced Red/Black Tree implementation.
This implements an intrusive balanced tree that guarantees O(log2(N)) runtime for all operations and amortized O(1) behavior for creation and destruction of whole trees. The algorithms and naming are conventional per existing academic and didactic implementations, c.f.:
https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
The implementation is size-optimized to prioritize runtime memory usage. The data structure is intrusive, which is to say the rbnode handle is intended to be placed in a separate struct, in the same way as with other such structures (e.g. Zephyr’s Doubly-linked list), and requires no data pointer to be stored in the node. The color bit is unioned with a pointer (fairly common for such libraries). Most notably, there is no “parent” pointer stored in the node, the upper structure of the tree being generated dynamically via a stack as the tree is recursed. So the overall memory overhead of a node is just two pointers, identical with a doubly-linked list.
Defines
-
RB_FOR_EACH(tree, node)
Walk a tree in-order without recursing.
While rb_walk() is very simple, recursing on the C stack can be clumsy for some purposes and on some architectures wastes significant memory in stack frames. This macro implements a non-recursive “foreach” loop that can iterate directly on the tree, at a moderate cost in code size.
Note that the resulting loop is not safe against modifications to the tree. Changes to the tree structure during the loop will produce incorrect results, as nodes may be skipped or duplicated. Unlike linked lists, no _SAFE variant exists.
Note also that the macro expands its arguments multiple times, so they should not be expressions with side effects.
- Parameters:
tree – A pointer to a struct rbtree to walk
node – The symbol name of a local struct rbnode* variable to use as the iterator
-
RB_FOR_EACH_CONTAINER(tree, node, field)
Loop over rbtree with implicit container field logic.
As for RB_FOR_EACH(), but “node” can have an arbitrary type containing a struct rbnode.
- Parameters:
tree – A pointer to a struct rbtree to walk
node – The symbol name of a local iterator
field – The field name of a struct rbnode inside node
Typedefs
-
typedef bool (*rb_lessthan_t)(struct rbnode *a, struct rbnode *b)
Red/black tree comparison predicate.
Compares the two nodes and returns true if node A is strictly less than B according to the tree’s sorting criteria, false otherwise.
Note that during insert, the new node being inserted will always be “A”, where “B” is the existing node within the tree against which it is being compared. This trait can be used (with care!) to implement “most/least recently added” semantics between nodes which would otherwise compare as equal.
Functions
-
static inline struct rbnode *rb_get_min(struct rbtree *tree)
Returns the lowest-sorted member of the tree.
-
static inline struct rbnode *rb_get_max(struct rbtree *tree)
Returns the highest-sorted member of the tree.
-
bool rb_contains(struct rbtree *tree, struct rbnode *node)
Returns true if the given node is part of the tree.
Note that this does not internally dereference the node pointer (though the tree’s lessthan callback might!), it just tests it for equality with items in the tree. So it’s feasible to use this to implement a “set” construct by simply testing the pointer value itself.
-
static inline void rb_walk(struct rbtree *tree, rb_visit_t visit_fn, void *cookie)
Walk/enumerate a rbtree.
Very simple recursive enumeration. Low code size, but requiring a separate function can be clumsy for the user and there is no way to break out of the loop early. See RB_FOR_EACH for an iterative implementation.
-
struct rbnode
- #include <rb.h>
Balanced red/black tree node structure.
-
struct rbtree
- #include <rb.h>
Balanced red/black tree structure.
Public Members
-
rb_lessthan_t lessthan_fn
Comparison function for nodes in the tree.
-
rb_lessthan_t lessthan_fn
-
RB_FOR_EACH(tree, node)